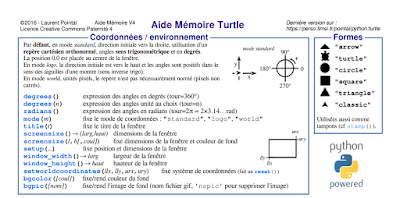
RetD SNT Turtle

 Dessine moi une étoile

L'objectif est de dessiner l'étoile de droite, avec le moins de lignes de code possible. Pour simplifier j'ai un peu agrandi l'étoile du haut pour que les branches tombent sur ma grille.

Pyhon, turtle et 1000 sapins

 

Vous êtes en seconde et vous aimez les arbres... alors testez ce script ;)

• le speed(10) c'est pour aller plus vite
• le if c'est pour éliminer le message d'erreur "division par 0"
• la formule pour c, c'est pour tenir compte de la perspective....

Mes beaux sapins de Noël, python et turtle

Objectif

Réaliser une forêt de sapins de Noël, comme c'est de saison... en python avec turtle. Pour la musique c'est ici! et pour se faire une idée de votre impact écologique si vous êtes partisan c'est là!

Pour les commandes, nous utiliserons :

• from turtle import * 
  pour la bibliothèque turtle
• dot()
  pour les points de départ des troncs
• setpos(x,y)
  pour aller à x,y
• import random as rd
  pour les commandes de la bibliothèque random
• randint(a,b)
  pour tirer un entier aléatoirement entre a et b
• penup()
  pour lever mon crayon et ne pas tracer de trait
• pendown()
  pour abaisser mon crayon et tracer des traits

Pour le mémo des commandes, voir ici:
https://perso.limsi.fr/pointal/_media/python:turtle:turtleref.pdf

python, turtle et création

Petit papier retrouvé en salle info. Dois-je y voir un message?

Notez la précision du trait. Je trouve cela joli, et je me demande s'il saurait ou si je saurais le faire en python...

Affaire à suivre...

Python fractal et turtle

Résultat

Script

import turtle
MINIMUM_BRANCH_LENGTH = 5
def build_tree(t, branch_length, shorten_by, angle):
  if branch_length > MINIMUM_BRANCH_LENGTH:
    t.forward(branch_length)
    new_length = branch_length - shorten_by
    t.left(angle)
    build_tree(t, new_length, shorten_by, angle)
    t.right(angle * 2)
    build_tree(t, new_length, shorten_by, angle)
    t.left(angle)
    t.backward(branch_length)
tree = turtle.Turtle()
tree.hideturtle()
tree.setheading(90)
tree.color('green')
build_tree(tree, 50, 5, 30)
turtle.mainloop()

Turtle, spirale et SNCF

En ce 12 novembre, quelque part sur la ligne entre Nantes et Montpellier, approche de la spirale pour ne pas perdre totalement la journée.

Et comme c'est inoui, je découvre:

• La ligne TGV et son WIFI inoui
  tiens je viens d'avoir un badge 300 km/h ;)))
• L'application GeoGebra en ligne

Etape 1 - le principe de construction avec GeoGebra

Avec GeoGebra cela donne ça:

Python et quête n°2 - Tables de multiplication et Mandelbrot

Objectif

Reproduire en python avec la bibliothèque turtle le genre de graphique de la vidéo du dessus car personnellement je trouve ça joli, voire "mathgique". Je suis à deux doigts d'imprimer des tee-shirts ;))))

Objectif atteins en ce 3 nov 2019 - 17:34
Et mise en musique constructiviste ici en ce 4 nov 2019 - 19:07

Couleurs aléatoires et traits avec Turtle

Objectif

Tracer des traits de couleurs aléatoires.

Script

from turtle import *
import random
colormode(255)
for i in range(500):
    r=random.randint(0, 255)
    v=random.randint(0, 255)
    b=random.randint(0, 255)
    color(r,v,b)
    fd(i)
    left(99)

Héron, Turtle et racine carrée

Script

from turtle import *
#encadrement racine de 2 et joli dessin avec turtle
#constante
s=2
color=["red","blue","green"] # liste des 3 couleurs des traits que turtle utilisera
#valeurs variables depart
a=8
b=s/a

# variable pour turtle
c=0 #initialisation des couleurs
imax=5 # nombre de boucles et donc nombre de figures
zoom=300
penup()
goto(-300,-300)
pendown()

#etape boucle
for i in range(imax):
    # methode heron calcul long et larg
    a=(a+b)/2
    b=s/a
    # choix d'une des trois couleurs
    if c>=3:
        c=c-3 
    pencolor(color[c])
    c=c+1
    # debut du dessin
    pendown()
    fd(a*zoom)
    left(90)
    fd(b*zoom)
    left(90)
    fd(a*zoom)
    left(90)
    fd(b*zoom)
    left(90)
    penup()

Application "Dans le secret des nombres" - le rangement des graines de tournesol

Présentation de l'application

Expérimentation inspirée par les pages 63-64 du livre "Dans le secret des nombres", livre que je vous conseille fortement. A la page 63 il est question du nombre d'or et de son existence dans la nature - voir les graines de tournesol.
Vous trouverez en dessous l'extrait du livre à partir de la page 63 ainsi qu'une vidéo et le script python utilisé pour approcher expérimentalement le grand mystère des graines de tournesol ;)

Extrait du passage du livre en dessous

Turtle - Créer une rosace avec 6 cercles et une boucle - version 2

Pour la version 1 voir ici
https://ptroulet.blogspot.com/2019/08/turtle-debuter-une-rosace-avec-trois.html

Script de la version 2

from turtle import *
# dessin des axes
home()
penup()
goto(-200,0)
pendown()
fd(400)
penup()
goto(0,-200)
pendown()
left(90)
fd(400)
penup()
home()

Turtle - Créer une rosace avec 6 cercles

Rosace avec ses 6 cercles + son cercle central

Construction

• Tracer les axes
• Tracer le premier cercle centré sur l'origine
• Parcourir sur 30° le premier cercle et placer un point
• Orienter la tortue de 90° sur un axe centrifuge
• S'éloigner du diamètre du cercle de la longueur du rayon
• Orienter la tortue tangentiellement au prochain cercle
• Tracer le cercle
• Retourner au centre (home)
• Pour les cercles suivants, ajouter 60° 
• Parcourir sur 30° + 60° sur le premier cercle et placer un point
• etc...

Suite à donner

• Insérer une boucle pour simplifier le code
  Voir ici
  https://ptroulet.blogspot.com/2019/08/turtle-creer-une-rosace-avec-6-cercles.html
• Utiliser les angles en les fonctions sinusoïdales pour généraliser la création de n cercles autour d'un cercle centrale

Turtle - Débuter une rosace avec deux cercles

Début de la rosace, il suffira de boucler avec d'autres cercles bleus

Construction

• Tracer les axes
• Tracer le premier cercle centré sur l'origine
• Parcourir sur 30° le premier cercle et placer un point
• Orienter la tortue de 90° sur un axe centrifuge
• S'éloigner du diamètre du cercle
• Orienter la tortue tangentiellement au prochain cercle
• Tracer le cercle

Turtle - Créer un hexagone avec des cercles

3 cercles donnent un hexagone

Source: Géométrie sacrée - Miranda Lundy

Construction

• cercle centré à l'origine
• 2ème cercle centré sur le périmètre du premier
• 3ème cercle centré à l'opposé du premier

=> Intersections axe X et cercles = Hexagone

Aide mémoire Turtle pour python

https://perso.limsi.fr/pointal/_media/python:turtle:turtleref.pdf

Lien de secours